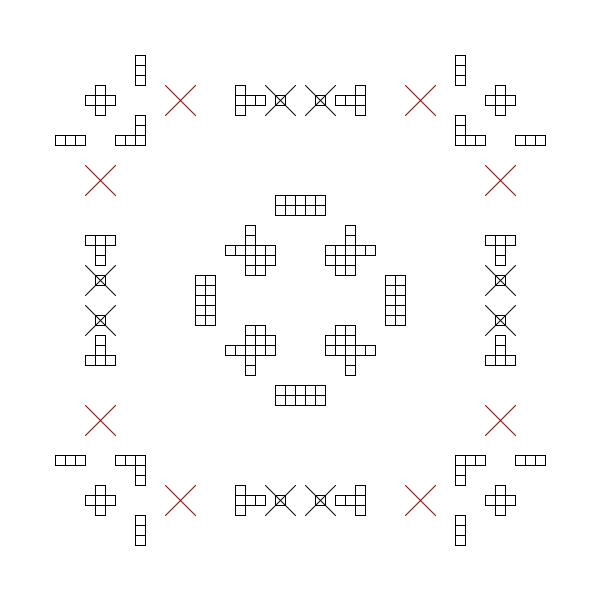
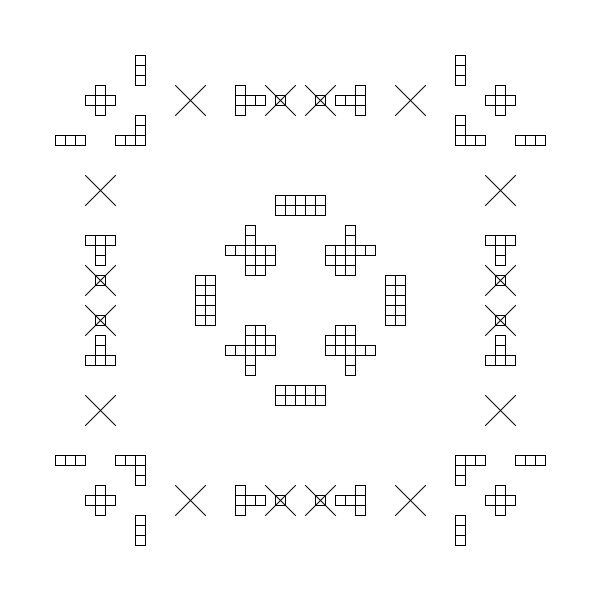Let's inspect and analyze carefully the pattern we got as a result after executing the rotations and the reflection:
The pattern is clearly divided into an inner and an outer part, furthermore the elements outside are all placed on the edges of a square:
The important question is, of course, how likely it is to have such an organized arrangement after performing the preceding operations. Obviously, the duplications and rotations themselves cause a high amount of symmetry (similarly to a kaleidoscope), as each item is octupled now. But is this effect (which, by the way, will not be exploited in the solution, as we will use only one quarter of the final figure) itself enough to explain the type of regularity we are observing here? Or, more precisely: what is the probability to get a similarly well-arranged pattern as a result after performing the rotational operations on an arbitrarily selected initial layout?
There are two approaches to answer these questions: practically (i.e. trial and error) and theoretically. Let's start with the first method, and carry out the operations on other layouts as well.
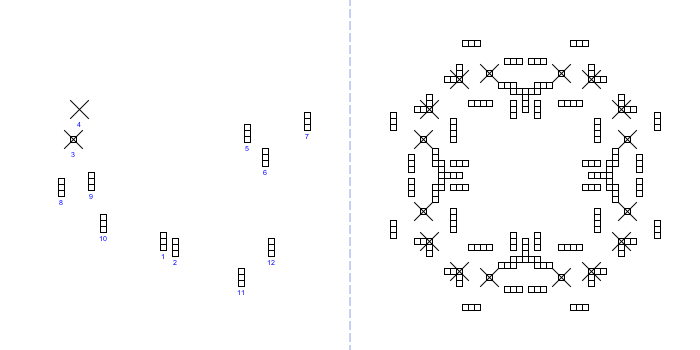
As I already mentioned in step 4, a separate Java application (PalenqueLayout) was created for this very purpose. With the help of it you can build different layouts, and then execute the rotations on them to check the final state (i.e. this control phase). To demonstrate that our initial layout is indeed a (very) special one, I'd like to present in the following some other layouts constructed with this program (more precisely they were composed by randomizing the default layout multiple times), that have the exact same items (10 triplets, 1 Sun and 1 star symbol), but placed at different positions. On the left side the initial state is shown, while on the right the end state after the rotations and reflection.
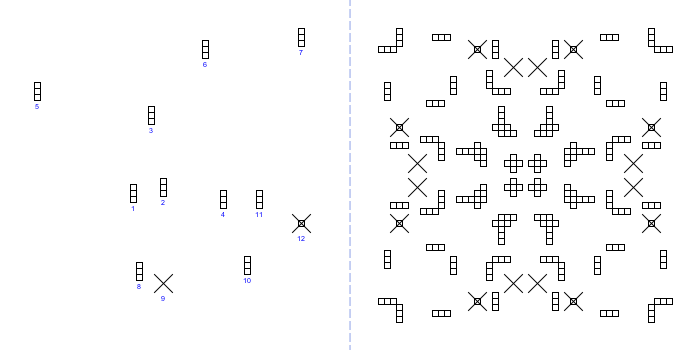
Layout #1 (PQLT9397T9898T9610T0896T7714T0521T2123T9484S9882T1285T1496R2192):
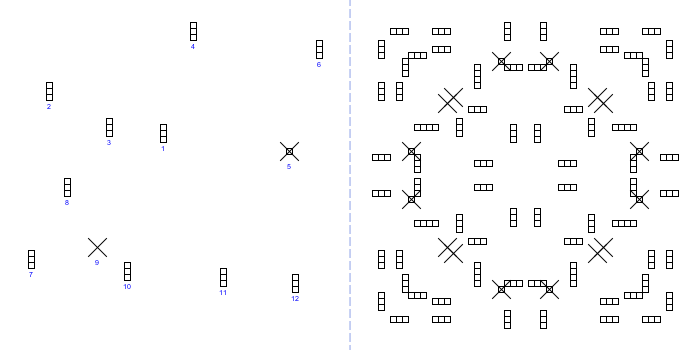
Layout #2 (PQLT9807T7914T8908T0324R1904T2421T7686T8298S8788T9284T0883T2082):
Layout #3 (PQLT9889T0088R8306S8411T1207T1503T2209T8198T8699T8892T1183T1688):
Note: These layouts were selected purely by chance, and the vast majority of the layouts are just very similar (in the sense of all being chaotic). With the PalenqueLayout utility you can rebuild and test these arrangements by importing the codes in parentheses, or you can also build new ones from scratch.
As we can see, the same "kaleidoscopical" symmetry, caused by the reflections themselves, can be noticed also here, but we don't recognize at all that organized and arranged appearance, that was observable at our initial layout above: there are no inner and outer parts separated, the items are not joined to larger shapes, there is no square to link the elements together, and so on.
So, it seems clear that our layout is indeed special to some extent: the question is, of course, exactly how special it is, how many other layouts could exist in theory with a similarly well-arranged control phase state. To be honest, giving a precise answer exceeds (by far) my mathematical abilities, and so I rather would let others, equipped with more advanced apparatus, compute this probability exactly, based on some geometrical framework (yet to be created?) for this and analogous coding systems.
Thus for now, until the theoretical background is clarified, we must settle for the practical approach, try different layouts by moving items around, and see whether we can arrive at any state as orderly as the one above. I myself have not been able to find any other layouts (aside from the variations of this of course) with even approximate (let alone same or exceeding) level of regularity, but encourage anybody interested in the subject to try this him/herself by using the PalenqueLayout utility (or by any other means). I personally am quite sure that the item arrangement on the lid is very (very) special if not unique, and to me this singularity is also a clear indication that the triplets are certainly not there for decoration purposes, but instead they were placed at their positions as constituent parts of a coding method, moreover by some beings with a very (very) high level of intelligence, since, presumably, we, present day humans ourselves would not manage to construct such a sophisticated encoding. But, of course, these are just intuitions and more (mainly theoretical) work is needed to obtain an absolute (or at least reasonable) assurance.
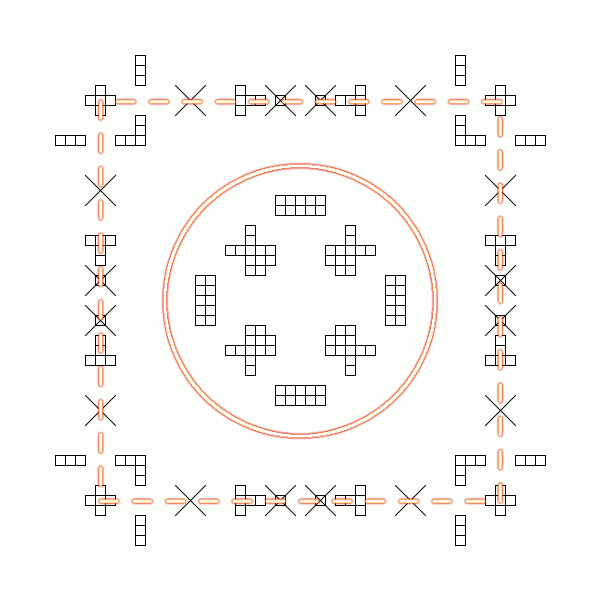
It also seems to be clear, that this control phase was included in the process by the designers in order to enable us, the decoders to correct the inaccuracies introduced by the representation. For this purpose the control phase is so sensitive (which is of course advantageous in this situation), that already moving one single item by only 1 or 2 units can easily break it. For example, in step 4 we have seen, that the Sun item (#11) did not cover completely the symbol under it, and so we could be tempted to move it one square to the left, from (−11, −20) to (−12, −20). But if we did so, the symmetry on the edge would be broken immediately, as the symbol would be closer now to the corners than to the middle elements:
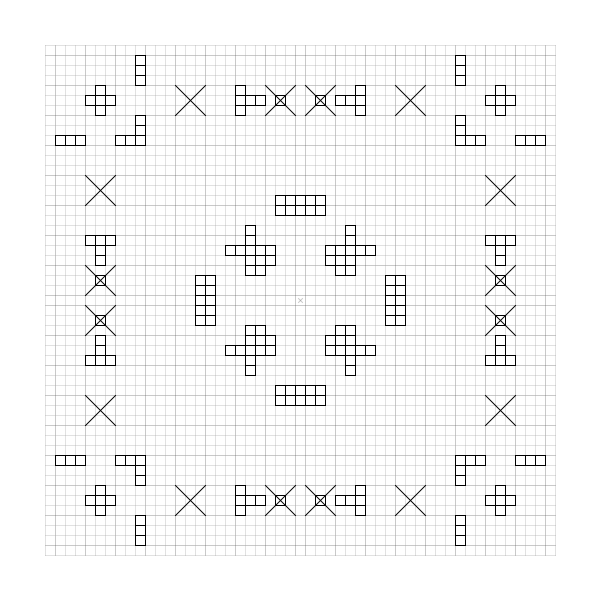
If we apply a 3×3-sized grid to the pattern, then it becomes immediately apparent, how symmetrical and well-ordered the outer edge is. Each element is located inside a 3×3-sized square, and also each gap has this size:
In this step we have thoroughly analyzed the control phase state, and have ascertained (to the degree achievable without a theoretically established framework for such types of encodings) that: 1. the layout presented in step 4 indeed seems be the closest one to the design originally conceived; 2. this reconstructed layout is so special (if not unique) with regard to the resulting state after performing the rotational operations, that it should make us at least suspicious about the explanation of the triplets being mere decorations, and should inspire us to go further in exploring the peculiarities of this pattern.
So, step after step it becomes more and more probable, that the code does really exist, and that we are on the right track to "crack" it. But we are only in the middle of the process, and certainly several new puzzles are there waiting for us. Let's see, whether we will be able to solve them too!